# 7. Logistics回归
# 分类
分类问题
- 电子邮件:是否垃圾邮件?
- 网上交易:是否欺诈交易?
- 肿瘤分类:是否良性/恶性?
分类可以二元分类,或者多分类,我们先从简单的negative/positive开始

如果我们尝试用线性回归来处理肿瘤的分类问题,用直线去拟合它,然后定义阈值为0.5,当h_θ(x)>=0.5,预测y为1;当h_θ(x)<0.5,预测y为0。
这样看上去这个算法能完美预测,但是当我们尝试新加个样本数据
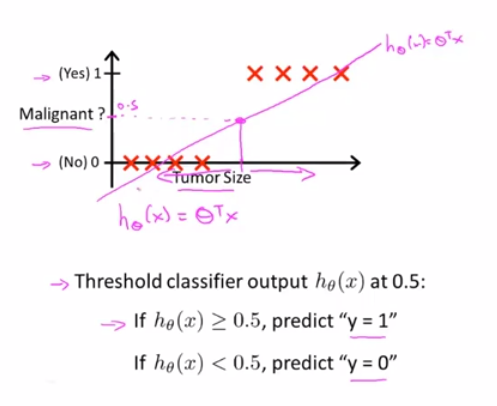
就会发现这个额外的样本数据,改变了原先拟合的直线,让原本恶性的样本被归类成良性了,所以把线性回归算法用于分类问题,并不是个好主意
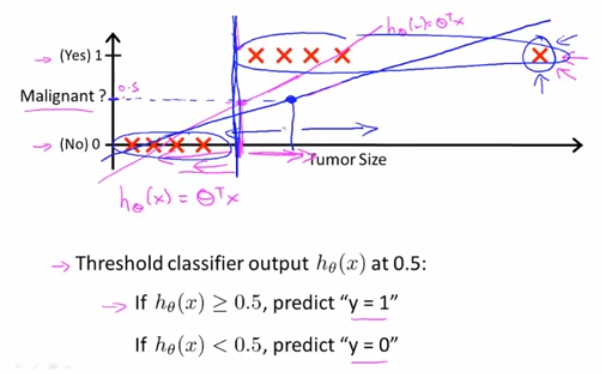
将线性回归算法引入分类问题,还会导致预测值和预期的分类输出不一致
所以我们将使用logistics回归算法来处理分类问题

# 假设表述
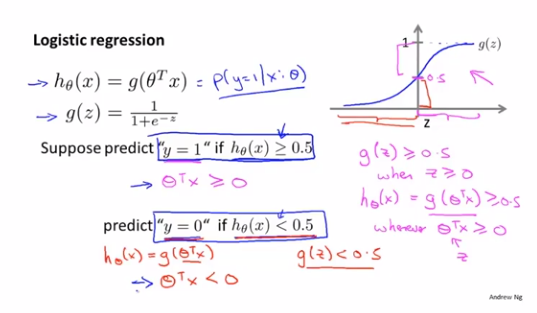
我们的假设函数是h_θ(x)=θ^T*x,现在希望分类器的输出值在[0,1]区间,我们可以令g(z)=1/(1+e^(-z)),g(z)可被称为sigmoid函数或logistics函数,可以看出g(z)的图像在原点左侧无限趋近于0,而在原点右侧无限趋近于1,那么我们将h_θ(x)作为参数代入g(z)可得h_θ(x)=1/(1+e^(-θ^T*x)),这样就可以确保原先h_θ(x)的输出分布在[0,1]区间了
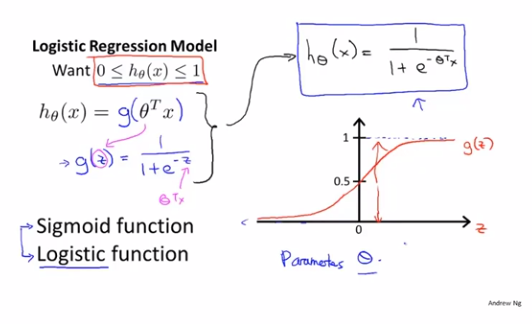
现在我们可以通过h_θ(x)来计算出y=1的概率,且由于y只能取0或1,所以y=0的概率+y=1的概率=1

# 决策界限
有了g(z)我们就可以将h_θ(x)输出假设定为0或1了
if h_θ(x) < 0.5 ? 0 : 1
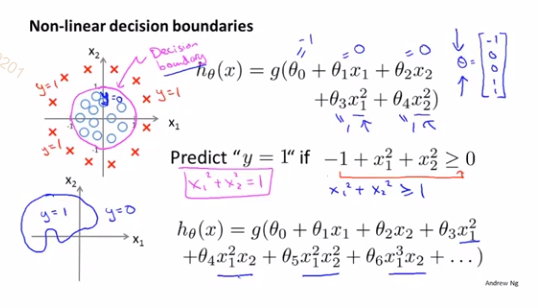
一个简单例子,x1+x2>=3的图像就是决策边界,在直线上方的点都被预测为y=1,下方反之
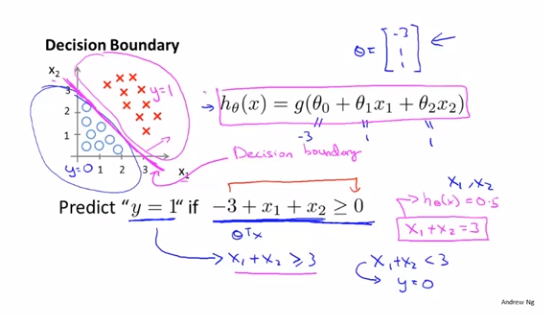
同上,只要我们计算出了θ,就能得出决策界限,而并不依赖图中根据训练集画出来的图像
复杂的假设函数能够更好地拟合决策边界图像